7 Pruebas inferenciales

Cuando trabajamos con tablas de contingencia es muy frecuente que sintamos la necesidad de tener que inferir acerca de la dependencia de las categorías analizadas o de las diferencias entre los grupos analizados. Siempre que nuestras variables cumplan con los requisitos que para ellas cada prueba establece (normalidad, homocedasticidad, linealidad y en algunos casos independencia), podremos aplicar las pruebas inferenciales típicas con tablas de contingencia en la investigación básica:

Chi² en su variantes de tabla y celda (Plackett 1983; Amón 2009 );
Pruebas z de contraste proporciones (Amón 2009; Glass et al. 1986 );
Prueba t de contraste de medias (Amón 2009; Glass et al. 1986 ).

Para todas ellasexpss nos da la oportunidad de hacer los cálculos desde el propio script de realización de la tabla y/o desde una instrucción posterior a la realización de la tabla. Pasemos por ello a explicar, no tanto el cometido de estas pruebas, sino el como llevarlas adelante.

7.1 Prueba de dependencia

El contraste Chi² de Pearson es una prueba estadística no paramétrica, que compara las frecuencias realmente obtenidas con las frecuencias esperadas que son las que corresponderían a cada celda o casilla de la tabla si su valor se ajustase a cualquier norma teórica previamente adoptada; en nuestro caso, una distribución proporcional de frecuencias normales Siegel, Castellan, et al. (1995). En definitiva, “se está calculando un índice acerca de la distancia entre lo real y lo esperado” Manzano Arrondo (1995).

El valor numérico de esta prueba se obtiene como:

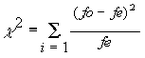
f_o, serán las frecuencias observadas en el experimento o muestra
f_e, serán las frecuencias esperadas teóricamente

Las frecuencias esperadas se calculan con …

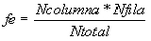
f_o, serán las frecuencias observadas en el experimento o muestra
f_e, serán las frecuencias esperadas teóricamente
N, es el número de efectivos muestrales

Esta prueba se suele utilizar (entre muchas otras posibilidades) para contrastar la hipótesis nula que los resultados obtenidos de una muestra no son significativos con relación a la población total, o bien como prueba de dependencia para comprobar la existencia o no de asociación entre las variables. En este caso, la prueba indica la existencia de asociación pero no la cuantifica Manzano Arrondo (1995).

7.1.1 De una tabla

La prueba Chi² puede hacerse a nivel de tabla, lo que muestra la relación de dependencia entre las categorías Siegel, Castellan, et al. (1995). Hagamos una primera aproximación con dos tablas de contingencia muy sencillas, pero que nos mostrarán como se indica que la relación de dependencia existe o no existe. La función tab_last_sig_cases realiza la prueba base de R denominada chisq.test.

Nótese el uso de “|”=unvr() para utilizar la variable sin que se publiquen los texto extra de la misma.

as.datatable_widget(
  data %>%
    tab_cols(total(), "|" = unvr(P31)) %>%
    tab_cells("|" = unvr(P2)) %>%
    tab_stat_cases() %>%
    tab_last_sig_cases() %>%
    tab_pivot()
)

Figura 7.1: Prueba Chi² en tabla

as.datatable_widget(
  data %>%
    tab_cols(total(), "|" = unvr(P31)) %>%
    tab_cells("|" = unvr(P33)) %>%
    tab_stat_cases() %>%
    tab_last_sig_cases() %>%
    tab_pivot()
)

Figura 7.1: Prueba Chi² en tabla

En la primera tabla se muestra la relación entre la variable P31 (sexo) y la P2 (valoración del sistema sanitario). Nótese que en la tabla se ha usado una línea tras el cálculo de los casos con la función tab_last_sig_cases() que indica que se debe realizar la prueba Chi² a la relación. Esta línea provoca que en la tabla surja una nueva fila sobre el #Total con el texto #Chi-squared p-value que indica que se realiza la prueba al 5% (0,05). Si el resultado es el rechazo de la hipótesis nula de independencia se muestra un <0,05 (warn.), pero si no se puede rechazar la hipótesis nula de independencia sale sólo (warn.) En la tabla no se publica el resultado de la prueba, pero podemos hacerlo siguiendo el formato estándar.

table(data$P2, data$P31)

##                                                               
##                                                                Hombre Mujer
##   En general, el sistema sanitario funciona bastante bien         277   261
##   El sistema sanitario funciona bien, aunque son necesarios al    620   627
##   El sistema sanitario necesita cambios fundamentales, aunque     288   349
##   Nuestro sistema sanitario está tan mal que necesitaríamos re     61    59
##   N.S.                                                              6     3
##   N.C.                                                              4     2

chisq.test(table(data$P2, data$P31))

## 
##  Pearson's Chi-squared test
## 
## data:  table(data$P2, data$P31)
## X-squared = 7.2669, df = 5, p-value = 0.2015

table(data$P33, data$P31)

##               
##                Hombre Mujer
##   Casado/a        677   711
##   Soltero/a       455   362
##   Viudo/a          41   149
##   Separado/a       24    33
##   Divorciado/a     55    42
##   N.C.              4     4

chisq.test(table(data$P33, data$P31))

## 
##  Pearson's Chi-squared test
## 
## data:  table(data$P33, data$P31)
## X-squared = 75.203, df = 5, p-value = 8.437e-15

Donde se puede observar que para la primera relación, no se puede rechazar la hipótesis de independencia pues el valor de significación es p-value > 0,05 (0.2015); para la segunda relación, sí podemos rechazar la hipótesis nula de independencia, puesto que p-value < 0,05 (por tanto, existe dependencia).

7.1.2 De una celda de una tabla

Particularmente de interés en investigación de mercados (de hecho solo está documentado su uso, y poco, en este ámbito) es la prueba Chi² de celda. A diferencia de la anterior, en este caso se realiza la prueba para cada celda de la tabla en particular. La lógica de la misma sería comparar un valor de la tabla (una celda), con el resto de su fila, el resto de su columna, y el resto de la muestra. De este forma, indicamos que valores son significativos en la tabla, aquellos que cabría contemplar con un interés especial.

Para obtener la tabla y la subsiguiente prueba se utilizará una nueva función denominada tab_last_sig_cell_chisq() sobre la misma estructura ya conocida de tabla. Nótese que en este caso, para la prueba se requiere utilizar los porcentajes en lugar de los casos, para que el cálculo sea el oportuno. Chi² es una prueba muy sensible al tamaño de la muestra.

as.datatable_widget(
  data %>%
    tab_cols(total(), "|" = unvr(P31)) %>%
    tab_cells("|" = unvr(P2)) %>%
    tab_stat_cpct() %>%
    tab_last_sig_cell_chisq() %>%
    tab_pivot()
)

Figura 7.2: Prueba Chi² de celda

as.datatable_widget(
  data %>%
    tab_cols(total(), "|" = unvr(P31)) %>%
    tab_cells("|" = unvr(P33)) %>%
    tab_stat_cpct() %>%
    tab_last_sig_cell_chisq() %>%
    tab_pivot()
)

Figura 7.2: Prueba Chi² de celda

La salida es muy clara. Con los símbolos mayor y menor, se marcan aquellas celdas que son significativamente mayores (>) o menores (<) que lo esperado y por tanto son las que direccionan las relaciones de dependencia que en la tabla se producen.

7.2 Pruebas de diferencias

Un conjunto diferentes de pruebas son aquellas cuya hipótesis de partida se basa en determinar si existen diferencias entre los porcentajes (prueba z) o las medias (prueba t) de dos grupos independientes en la muestra extraídos de la misma población. Desarrollamos ambas pruebas en las líneas siguientes.

7.2.1 Porcentajes (prueba z)

Asumiendo las hipótesis necesarias para poder trabajar con estadística paramétrica (normalidad, homocedasticidad, linealidad y en algunos casos independencia), la función tab_last_sig_cpct realiza z-test entre columnas de porcentajes derivadas de la aplicación de tab_stat_cpct. Los resultados son calculados con la misma fórmula que con la función base de R prop.test y sin la corrección de continuidad.

Obsérvese la diferencia de concepto; mientras que la prueba Chi² de celda realiza la prueba comparando con el marginal total, la prueba z realiza esa comparación entre los grupos formados por las columnas, a los que se suele llamar perfiles. De esta forma considera la independencia de los grupos muestrales entre sí.

Para utilizar esta funcionalidad el script sería el siguiente:

as.datatable_widget(
  data %>%
    tab_cols(total(), "SEXO" = unvr(P31)) %>%
    tab_cells("|" = unvr(P2)) %>%
    tab_stat_cpct() %>%
    tab_last_sig_cpct() %>%
    tab_pivot()
)

Figura 7.3: Prueba Z en tabla

as.datatable_widget(
  data %>%
    tab_cols(total(), "SEXO" = unvr(P31)) %>%
    tab_cells("|" = unvr(P33)) %>%
    tab_stat_cpct() %>%
    tab_last_sig_cpct() %>%
    tab_pivot()
)

Figura 7.3: Prueba Z en tabla

En nuestro caso, los resultados son muy semejantes a los vistos con Chi² de celda, porque la variable elegida para las columnas es dicotómica, es decir, con sólo dos opciones de respuesta, exhaustivas y mutuamente excluyentes. No sería así si la variable de columnas presentara más de 2 perfiles.

La lectura de esta prueba es la siguiente. El porcentaje de casos en en el grupo B (mujeres) de la tabla 1, es significativamente más elevado que el de hombres, determinándose esta diferencia con una significación del 5%. En el caso de la tabla 2, el porcentaje de hombres solteros es significativamente diferente del porcentaje de mujeres solteras. Del mismo modo y a la inversa el porcentaje de mujeres viudas entrevistadas en la muestra es significativamente mayor que el de hombres.

Por tanto, creemos que queda claro el funcionamiento de la prueba. Se etiquetan las columnas y se muestra la letra de la columna con la que se presentan diferencias positivas junto al valor porcentual. La prueba se realiza para cada celda, pero siempre comparando con las celdas que tiene a su derecha o izquierda en la misma fila (no con el total).

7.2.2 Medias (prueba t)

Al igual que en el apartado anterior el objetivo es determinar si existen o no diferencias entre los grupos que se están testando, teniendo como hipótesis nula que las medias de los grupos son iguales. En nuestro ejemplo, hemos tomado la de auto clasificación ideológica (recodificando las posiciones de 1 a 10, izquierda a derecha respectivamente) creando grupos de izquierda, centro y derecha. Sobre esta tabla que calcula las medias, se aplica el estadístico tab_stat_mean_sd_n()que contiene todos los datos requeridos para el cálculo del valor t y se le indica que requerimos el test con tab_last_sig_means(). Se asume que los grupos son independientes, que existe normalidad y que las varianzas de los grupos son iguales.

as.datatable_widget(
  data %>%
    tab_cols(
      total(),
      P29 = recode(
        P29,
        "Izquierda" = 1:4 ~ 1,
        "Centro" = 5:6 ~ 2,
        "Derecha" = 7:10 ~ 3,
        TRUE ~ NA
      )
    ) %>%
    tab_cells(P3 = na_if(P3, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means() %>%
    tab_pivot()
)

Figura 7.4: Prueba t en tabla

Se puede observar que la salida es igual a la de la prueba Z. Se rotulan las columnas con las letras A, B … y las que sean necesarias, y posteriormente se muestra (por defecto) la letra de la columna con la que la media de la columna en la que se ubica la media presenta diferencias positivas (es mayor). Podemos por tanto observar, que en la población de la que se ha extraído la muestra, se puede afirmar que la media de satisfacción con el funcionamiento del sistema sanitario español es más alta en los individuos cuya auto clasificación ideológica es del grupo de derecha (C), que en la izquierda (A) y en el centro (B). No entramos a valorar si la distribución de grupos es la correcta o no, en cuanto al significado general. Se ha hecho una distribución acorde al significado de los números en sí mismos.

Existen ocasiones en las que esta prueba, se requiere publicar para un conjunto de ítems que forman parte de una misma batería. En estos casos, no es tan interesante publicar las desviaciones y las bases, por lo que podemos formular de esta forma el script.

as.datatable_widget(
  data %>%
    tab_cols(
      total(),
      P29 = recode(
        P29,
        "Izquierda" = 1:4 ~ 1,
        "Centro" = 5:6 ~ 2,
        "Derecha" = 7:10 ~ 3,
        TRUE ~ NA
      )
    ) %>%
    tab_cells(P901 = na_if(P901, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_cells(P902 = na_if(P902, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_cells(P903 = na_if(P903, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_cells(P904 = na_if(P904, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_cells(P905 = na_if(P905, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_cells(P906 = na_if(P906, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_cells(P907 = na_if(P907, gt(10))) %>%
    tab_stat_mean_sd_n() %>%
    tab_last_sig_means(keep = "means") %>%
    tab_pivot()
)

Figura 7.5: Prueba t con sólo medias

Se puede observar que la instrucción keep="means" lo que ha conseguido es eliminar la publicación de la desviación y la media del cuadro presentado. De este modo el resultado es más compacto y da una visión general de la batería de ítems

7.3 Parámetros posibles en las pruebas de significación

De manera conjunta exponemos aquí diferentes parámetros que modifican el comportamiento por defecto de las cuatro pruebas anteriormente vistas. Algunos son de uso en todas ellas y otros específicos de alguna de las pruebas.

sig_level, numérico; nivel de significación, por defecto es igual a 0.05.
min_base, numérico; el test de significación se realizará si ambas columnas tienes bases mayores o iguales al valor determinado que por defecto es 2.
delta_cpct, numérico; delta mínimo entre el porcentaje para el que marcamos diferencias significativas (en puntos porcentuales); de forma predeterminada, es igual a cero. Tenga en cuenta que, por ejemplo, para una diferencia mínima de 5 por ciento de puntos, delta_cpct debe ser igual a 5, no 0.05.
delta_means, numérico; delta mínimo entre medias para las que marcamos diferencias significativas: por defecto es igual a cero.
correct, lógico (TRUE o FALSE), indica si aplicar corrección de continuidad al calcular el estadístico Chi² de prueba para tablas de 2 por 2. Solo para significance_cases y significance_cell_chisq. Para más detalles ver chisq.test. TRUE por defecto.
compare_type tipo de comparación por columnas. Por defecto, es subtabla (variable por variable). otras posibilidades son first_column, adjusted_first_column y previous_column; podemos realizar varios test simultáneamente.
bonferroni lógico; FALSE por defecto; uso del ajuste de Bonferroni por cada fila.
subtable_marks, carácter; una de las siguientes opciones: greater, both or less; por defecto se marcan sólo valores cuya significación sea mayor (greater) que alguna otra columna. Para significance_cell_chisq por defecto es both. podemos modificar este comportamiento usando las otras alternativas.
inequality_sign lógico. FALSE si subtable_marks es menor o mayor. Debemos mostrar > o < antes de las marcas de importancia de las comparaciones de subtabla.
sig_labels etiquetas de vector de caracteres para marcar diferencias entre columnas de subtabla.
sig_labels_previous_column un vector de caracteres con dos elementos. Etiquetas para marcar una diferencia con la columna anterior. La primera marca significa menor (por defecto es v) y la segunda significa mayor (^).
sig_labels_first_column un vector de caracteres con dos elementos. Etiquetas para marcar una diferencia con la primera columna de la tabla. La primera marca significa menor (por defecto es -) y la segunda significa mayor (+).
sig_labels_chisq un vector de caracteres con dos etiquetas para marcar una diferencia con el margen de fila de la tabla. La primera marca significa menor (por defecto es <) y la segunda significa mayor (>). Solo para Meaning_cell_chisq.
keep, carácter. Una o más de las siguientes percent, cases, means, bases, sd o none. Este argumento determina qué estadísticos permanecerán en la tabla después del marcado de significación.
row_margin, carácter. Uno de los valores auto (predeterminado), sum_row o first_column. Si es auto, tratamos de encontrar la columna total en la subtabla por total_column_marker. Si la búsqueda falla, usamos la suma de cada fila como total de filas. Con la opción sum_row siempre sumamos cada fila para obtener margen. Tenga en cuenta que en este caso el resultado de las variables de respuesta múltiple en la cabecera puede ser incorrecta. Con la opción first_column usamos la tabla primera columna como margen de fila para todas las subtablas. En este caso, el resultado de las subtablas con bases incompletas puede ser incorrecto. Solo para significance_cell_chisq.
total_marker, carácter. Total de fila marcado en la tabla. # por defecto.
total_row, entero/carácter. En el caso de varios totales por subtabla, es un número o nombre de fila total para el cálculo de significación.
digits, un número entero que indica cuántos dígitos después del separador decimal se mostrarán en la tabla final.
na_as_zero, lógico; FALSE por defecto. ¿Deberíamos tratar a NA como cero casos?
var_equal, lógico; variable que indica si se deben tratar las dos varianzas como iguales. Para más detalles ver t.test.
mode, carácter; replace (default) o append. En el primer caso, el resultado anterior en la secuencia del cálculo de la tabla se reemplazará con el resultado de la prueba de significación. En el segundo caso, el resultado de la prueba de significación se agregará a la secuencia del cálculo de la tabla.
label, carácter; etiqueta para la estadística en tab_*. Ignorado si el modo es igual a replace.
total_column_marker, carácter; marca para la columna de totales en las subtablas. # por defecto.
x table (class etable): resultado de cro_cpct con proporciones y bases para significance_cpct, resultado de cro_mean_sd_n con medias, desviaciones estándar y N válido para significance_means, y resultado de cro_cases con recuentos y bases para significance_cases.
cases_matrix, matriz numérica con recuentos de tamaño filas*columnas.
row_base, vector de números con las bases de fila.
col_base, vector de números con las bases de columna.
total_base, número con la base total.

7.3.1 Algunos ejemplos de uso de los parámetros

Cambio del nivel de significación de la prueba y eliminación de las filas con las frecuencias, entre otros…

as.datatable_widget(
  data %>%
    tab_cols(total(), "|" = unvr(P31)) %>%
    tab_cells("|" = unvr(P33)) %>%
    tab_stat_cases() %>%
    tab_last_sig_cases(
      sig_level = 0.01,
      correct = TRUE,
      keep = "bases",
      mode = "replace",
      label = "***"
    ) %>%
    tab_pivot()
)

Figura 7.6: Prueba Chi² con significación al 99%

7.4 Conclusión al uso del paquete expss

Hemos presentado de forma muy breve y simplificada como podemos aprovechar toda la potencia de expss en nuestros scripts. Lo importante es practicar y practicar. No dejes de acudir a las viñetas de ayuda de Gregory Demin acerca de como usar el paquete y como generar nuevas tablas. Nosotros tan sólo hemos sentado las bases. Combinando las tablas con lenguaje R se puede llegar a conseguir casi todo.

Hasta aquí llegamos.

Bibliografía

Amón, Jesús. 2009. Estadı́stica Para Psicólogos. Madrid: Pirámide, 1990.

Glass, Gene V, Julian C Stanley, Elsa Galvis Gómez, and Eugenia Guzmán. 1986. Métodos Estadı́sticos Aplicados a Las Ciencias Sociales. Prentice-Hall Hispanoamericana.

Manzano Arrondo, Vicente. 1995. Inferencia Estadística: Aplicaciones Con SPSS/PC+.

Plackett, R. L. 1983. “Karl Pearson and the Chi-Squared Test.” International Statistical Review / Revue Internationale de Statistique 51 (1): 59–72. http://www.jstor.org/stable/1402731.

Siegel, Sidney, N John Castellan, et al. 1995. Estadı́stica No Paramétrica: Aplicada a Las Ciencias de La Conducta. Vol. 4. Trillas México.